Durch die Bildung von gleitenden Durchschnitten erhält man eine
Glättung der zugrundeliegenden Kursreihe. Man kann den Trend
der Kursentwicklung leichter erkennen.
Die Vorschrift für die Berechnung eines gleitenden Durchschnitts
mit arithmetischen Mittelwerten für 10 Tage lautet:
GDAM(t) = (KURS(t) + KURS(t-1) + ... + KURS(t-9)) / 10
GDAM(t) : GD arithmetisch für Tag t
KURS(t) : Kurs für Tag t
Falls die Kursentwicklung den etwa waagrechten GD von unten
nach oben schneidet, so wird dies als Kaufsignal gewertet.
Entsprechend wird ein Schnitt des annähernd waagrechten GD
durch die Kurswerte von oben nach unten als Verkaufsignal
eingestuft.
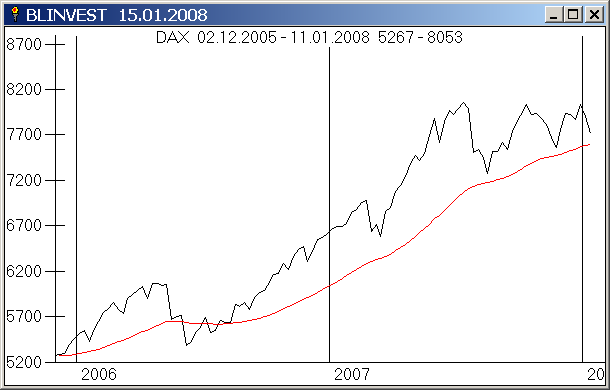
Gleitender Durchschnitt (8 Wochen) arithmetisch für DAX :
Ein GD mit linear gewichteten Mittelwerten für 5 Tage wird
folgendermaßen berechnet:
GDGM(t) = (5 KURS(t) + 4 KURS(t-1) + ... + 1 KURS(t-4)) /
( 5 + 4 + 3 + 2 + 1)
GDGM(t) : GD lin. gewichtet für Tag t
KURS(t) : Kurs für Tag t
Die Interpretation des GD gewichtet erfolgt genauso wie für den
GD arithmetisch Wobei jedoch zu beachten ist, daß der GD gewichtet auf
aktuelle Kursänderungen, wegen der stärkeren Gewichtung schneller
reagiert als der GD arithmetisch
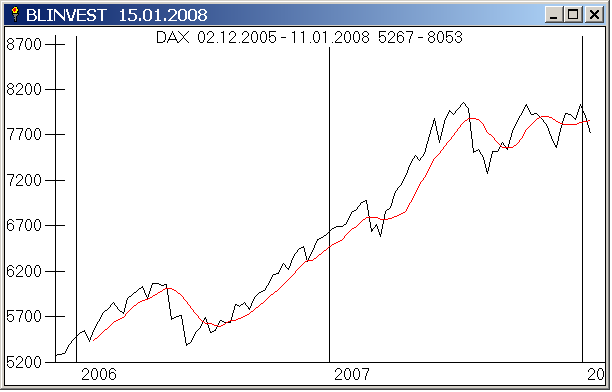
Gleitender Durchschnitt (8 Wochen) gewichtet für DAX :
Der GD exponentiell wird mit Hilfe eines Glättungsfaktors L
berechnet:
GDEXP(t) = L * KURS(t) + (1-L) * GDEXP(t-1)
GDEXP(t) : GD exponentiell für Tag t
KURS(t) : Kurs für Tag t
Der GD exponentiell ist eine Näherung für den GD arithmetisch falls
man L bestimmt durch:
L = 2 / m
L : Glättungsfaktor
m : Anzahl Zeitperioden (Tage) für GD arithmetisch
Falls man bei Wochenschlußkursen m = 40 wählt, dann erhält man den bekannten 200 Tage-Durchschnitt.
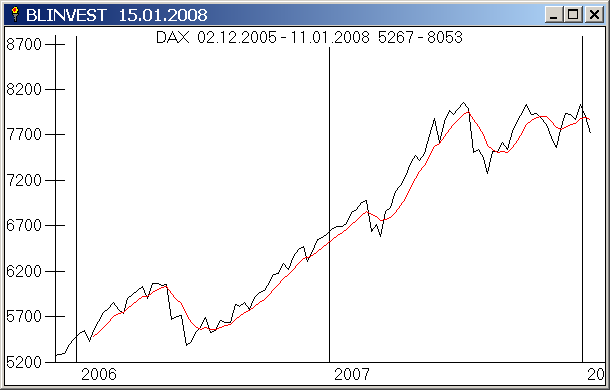
Gleitender Durchschnitt (40 Wochen) exponentiell für DAX :